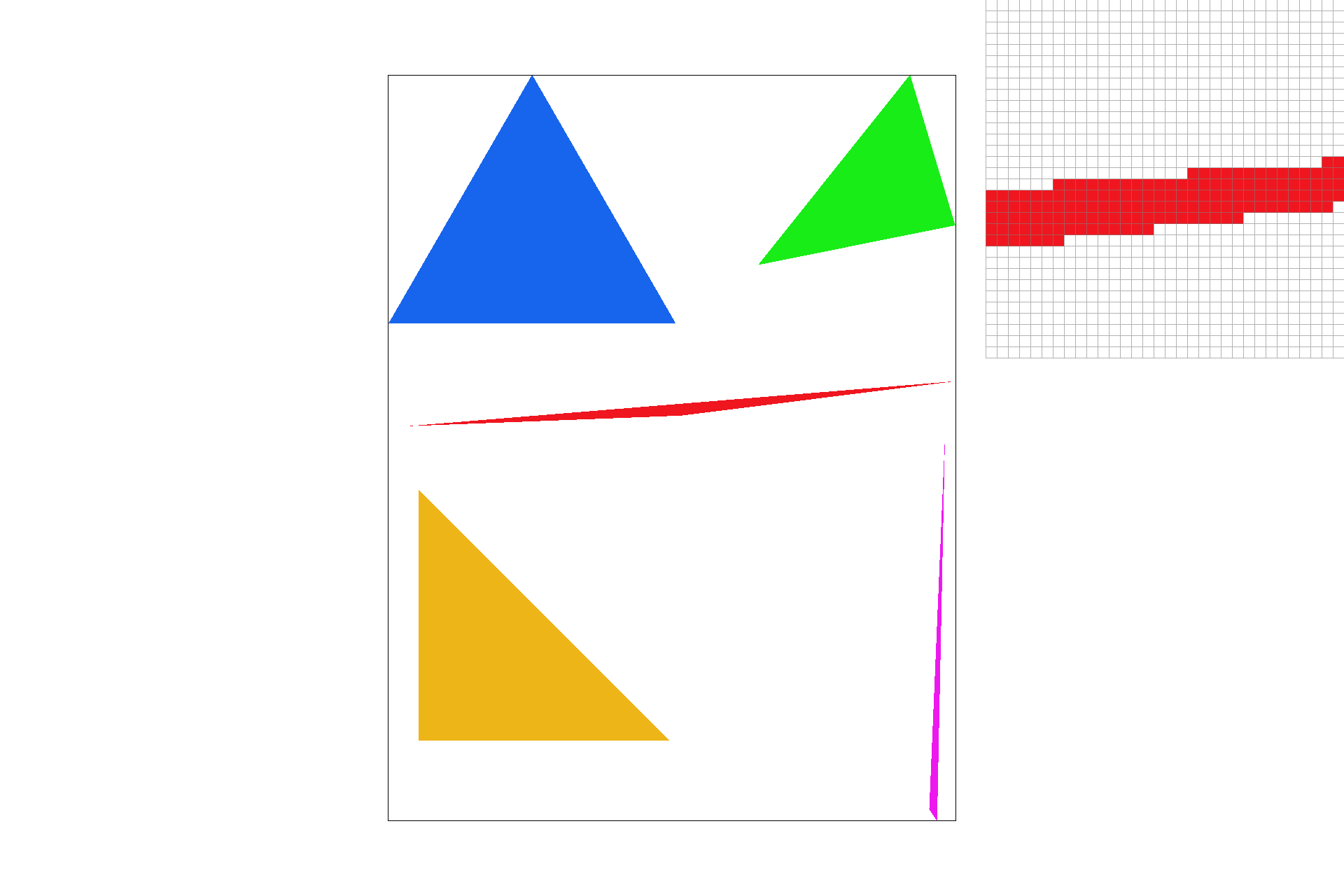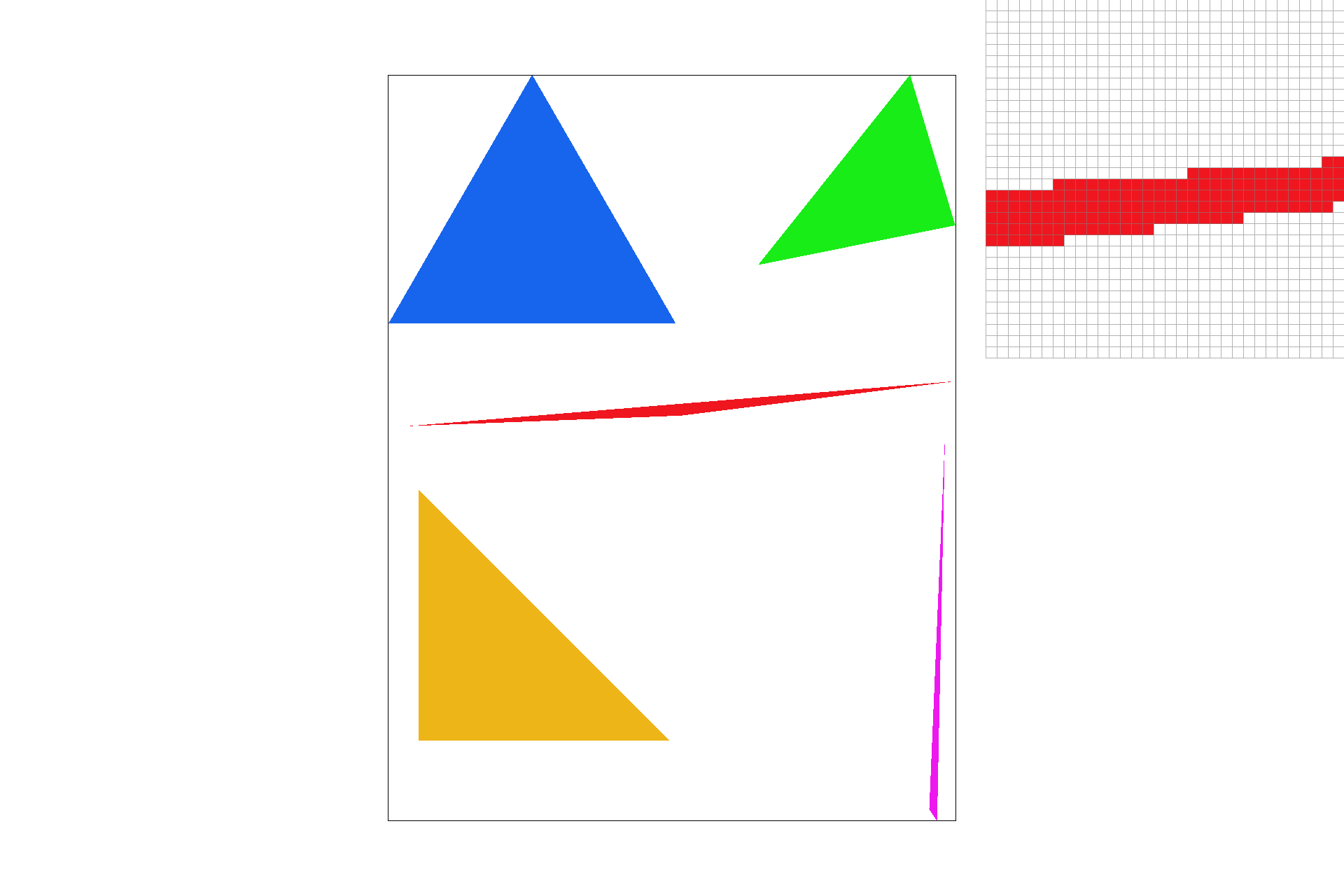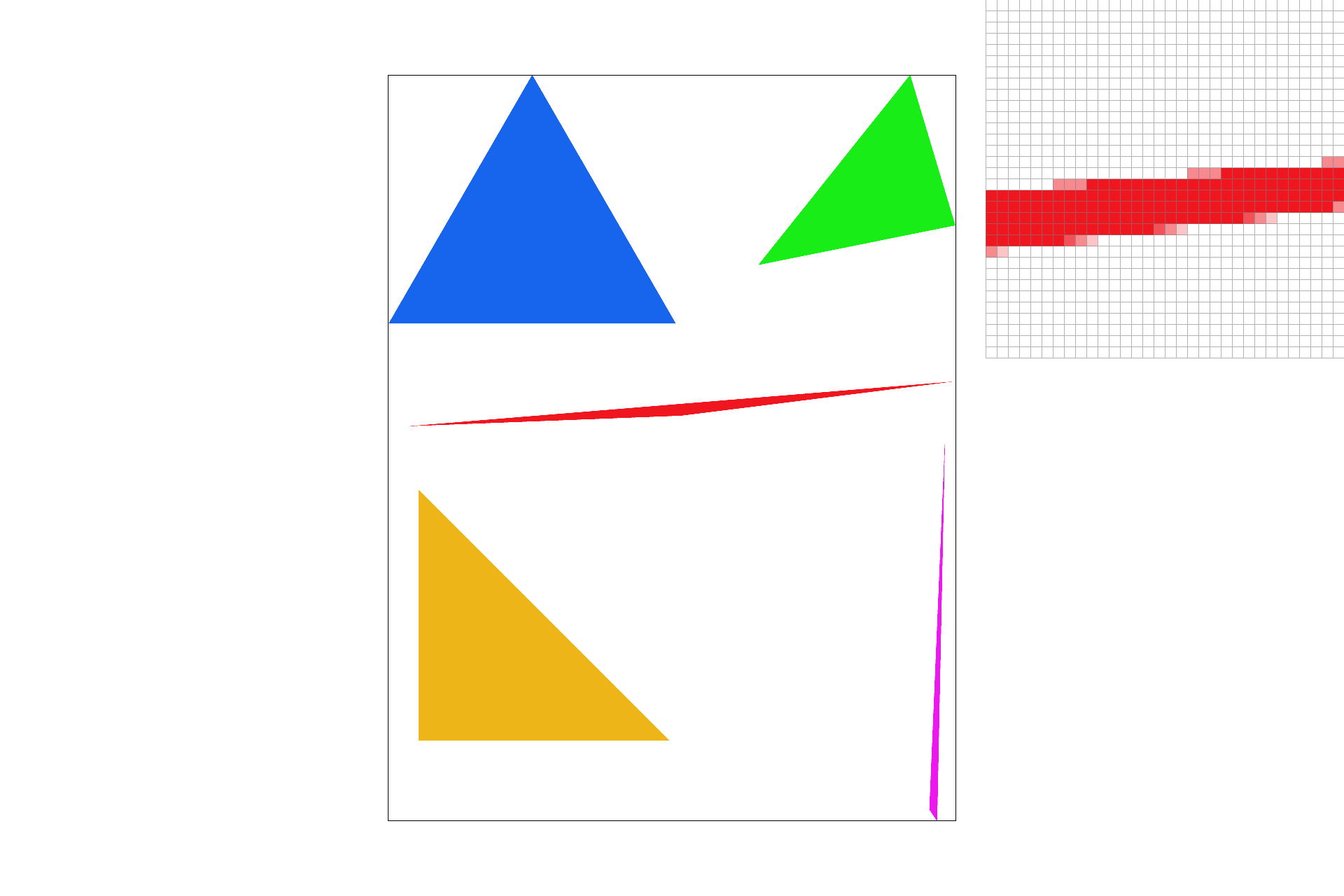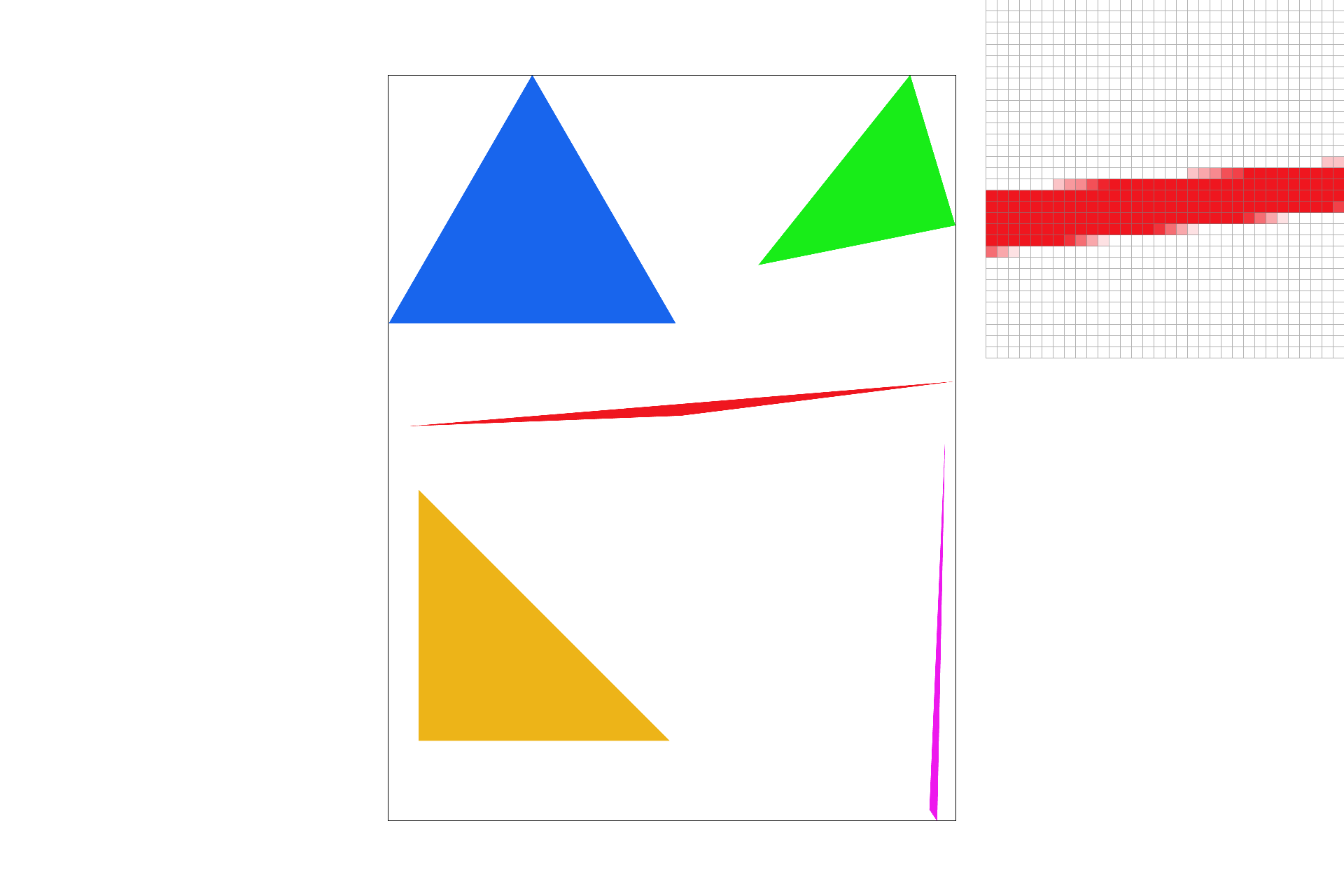Overview
In this project, I implemented basic functionalities of a rasterizer. A rasterizer, when given sets of coordinates will render images on a flat screen, even an object in a 3D space. The project began with basic rasterization, using line tests to fill in triangles by taking one sample per pixel. The next part involved supersampling, taking multiple samples per pixel and averaging out the colors. Next, I completed transform functions to scale, rotate, and translate the images. I used barycentric coordinates to help calculate the average color in part of an image. Barycentric coordinates are weights that can help determine where a point lies relative to other verticies. Since I am a regular user of 3D software such as Maya, I enjoyed the texture mapping section of the project. I took the coordinates of pixels from the screen space and mapped those to pixels in the texture space. Finally, after implementing bilinear sampling and nearest-neighbor sampling, I added level-sampling functionalities with mipmap.
Section I: Rasterization
Part 1: Rasterizing single-color triangles
The first part of this project includes the rasterization of single-colored triangles. With three given (x, y) coordinates I performed point-in-triangle tests using the line equation to determine whether each pixel is inside the bounds of the triangle. One problem I ran into was initially assuming that the points are given in clockwise order, which may not always be the case. After this realization, I included more point-in tests to ensure that the rasterizer is compatible with points that are not necessarily given in clockwise order(ex: if the line equation for all 3 lines and a given point returns something less than 0). Something I changed, when rasterization became fairly slow for some images, was only checking pixels inside the bounding box of each triangle. Thus, my algorithm is no slower than one that also rasterizes using bounding boxes.
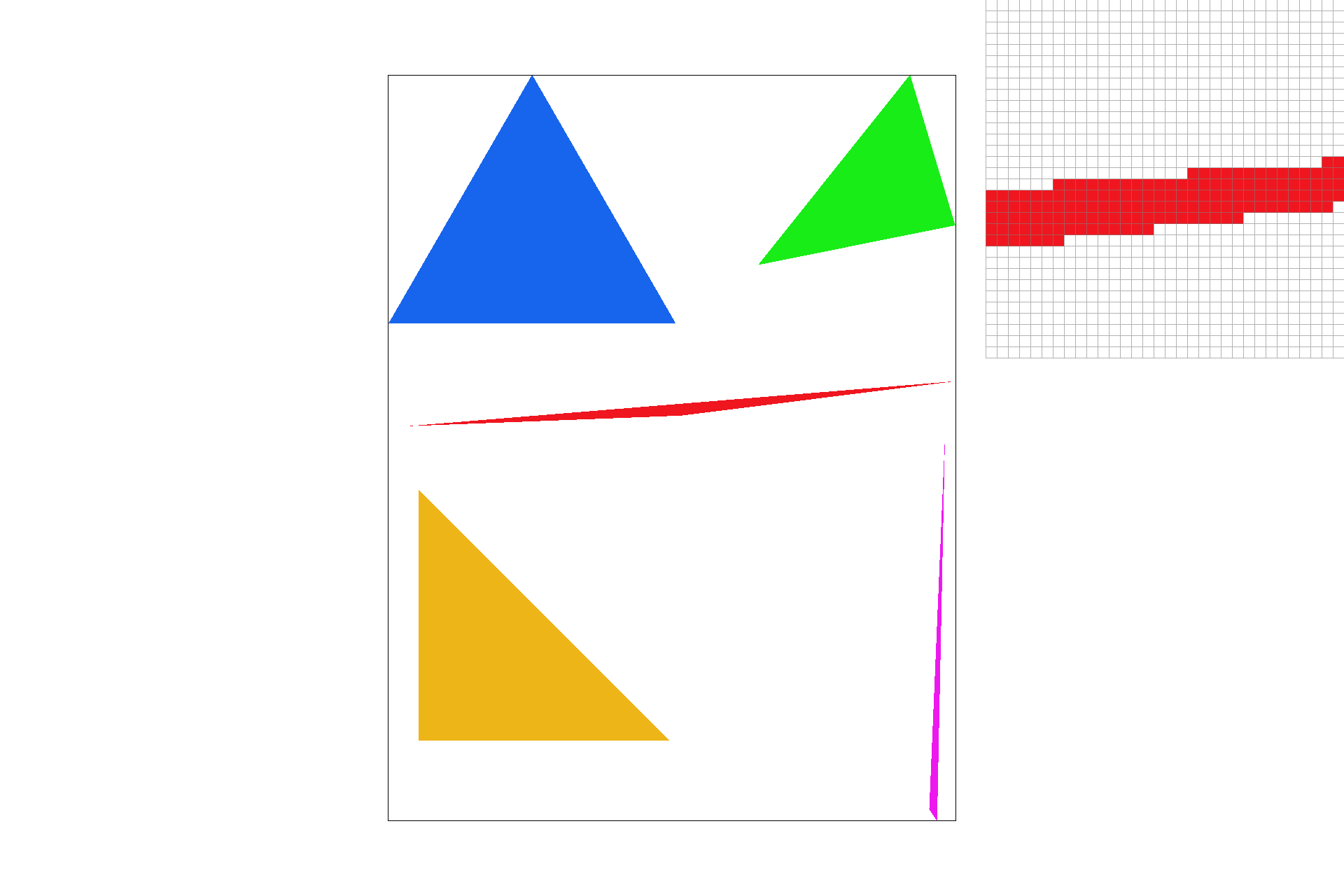 basic/test4.svg
basic/test4.svg
|
 basic/test6.svg
basic/test6.svg
|
 basic/test5.svg
basic/test5.svg
|
 basic/test3.svg
basic/test3.svg
|
Part 2: Antialiasing triangles
In part 2, I implemented supersampling. By sampling more than once per pixel, we can get a more accurate and smoother image (less aliasing). Similar to the sampling of each pixel, I performed the same point-in-triangle tests at the center of each sub-pixel. After determining which sub-pixels were in the bounds of of the triangle, the number of filled in samples in each pixel were averaged to determine the new total RGB value of that pixel. Thus, supersampling allows us to create less jagged images with smoother boundary transitions between colors. Calculating the exact center point of each pixel proved to be tricky. After the completion of supersampling, however, I realized how necessary it is to be completely accurate with subpixel centers for the purpose of averaging colors.
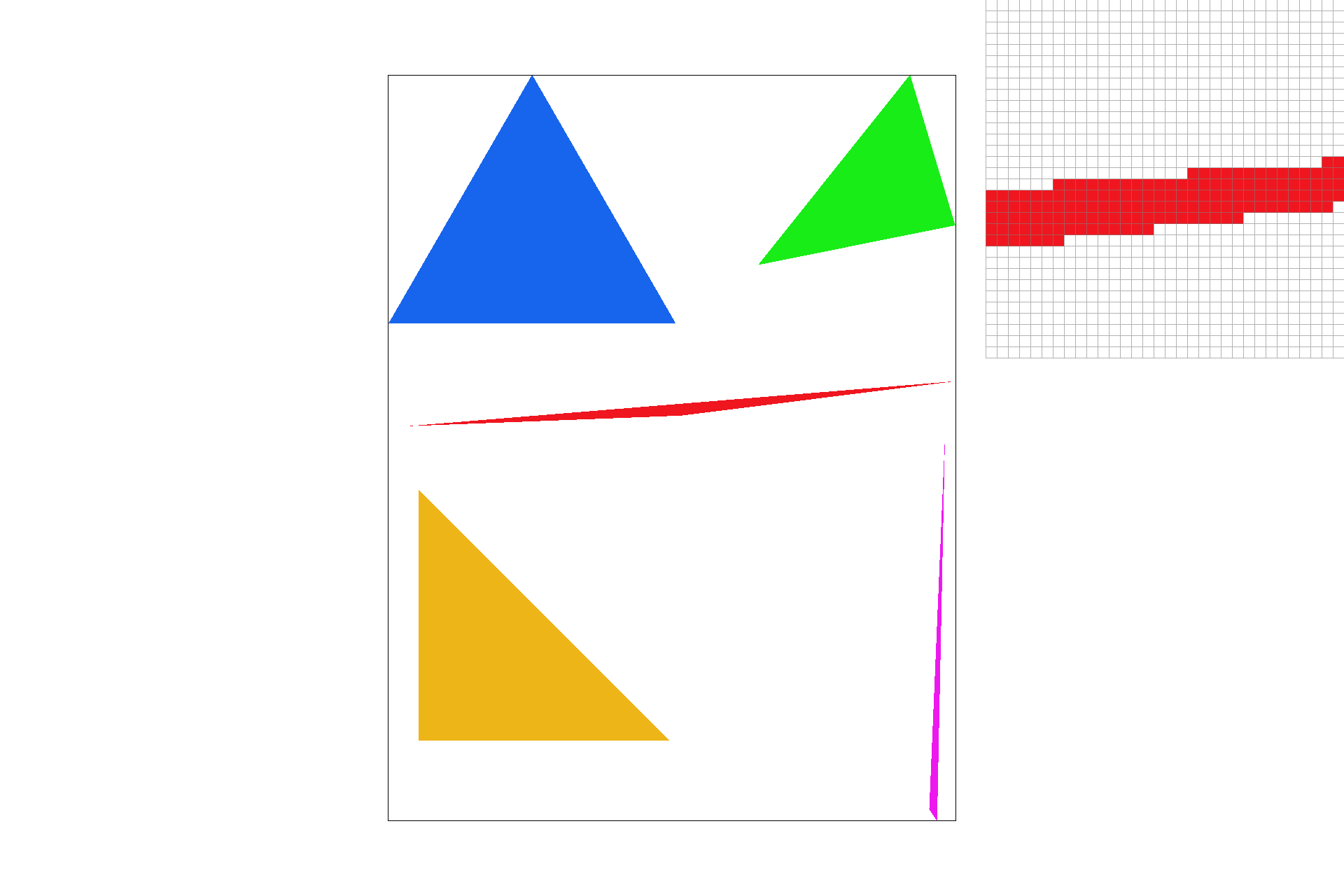 basic/test4.svg with sample rate of 1
basic/test4.svg with sample rate of 1
|
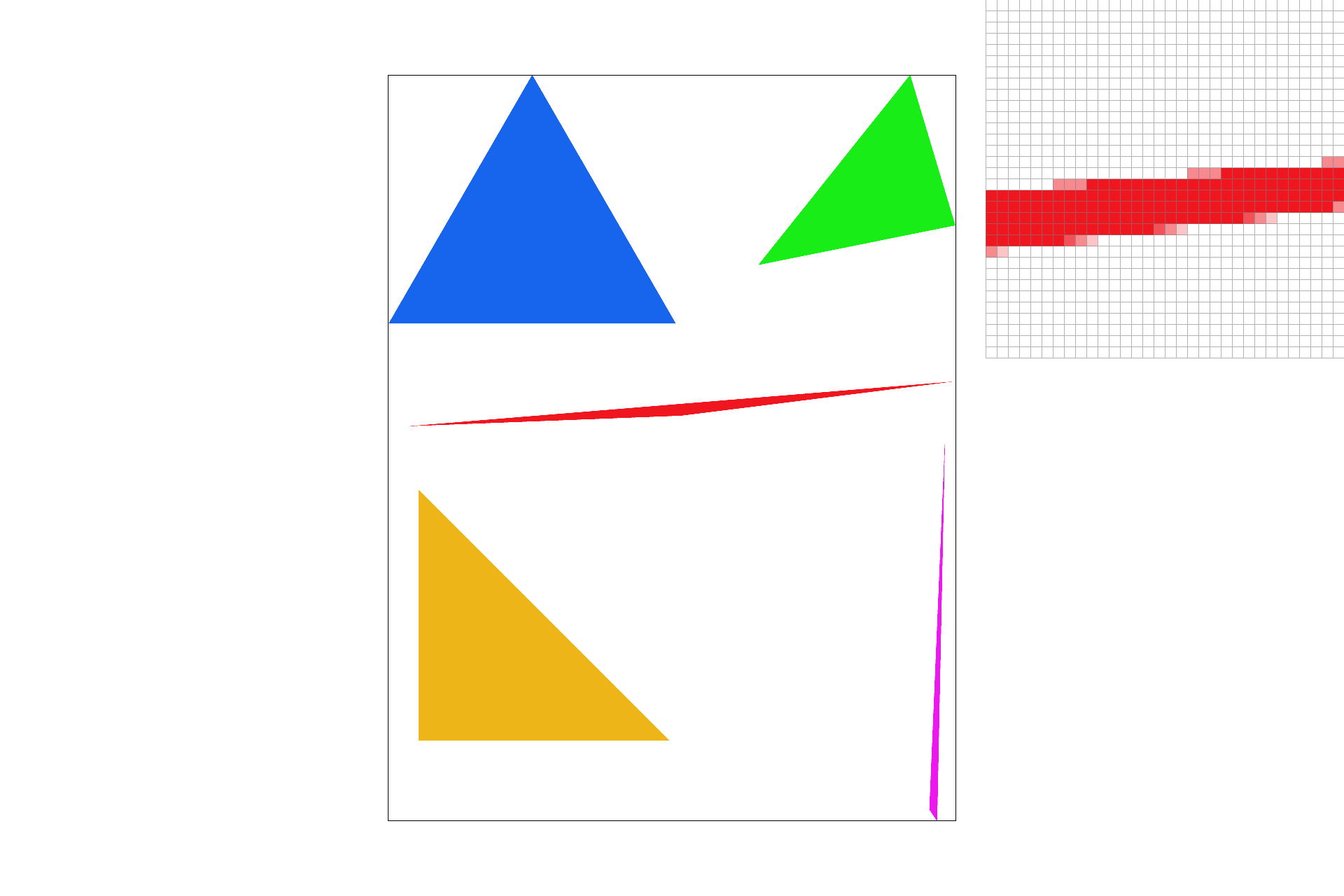 basic/test4.svg with sample rate of 4
basic/test4.svg with sample rate of 4
|
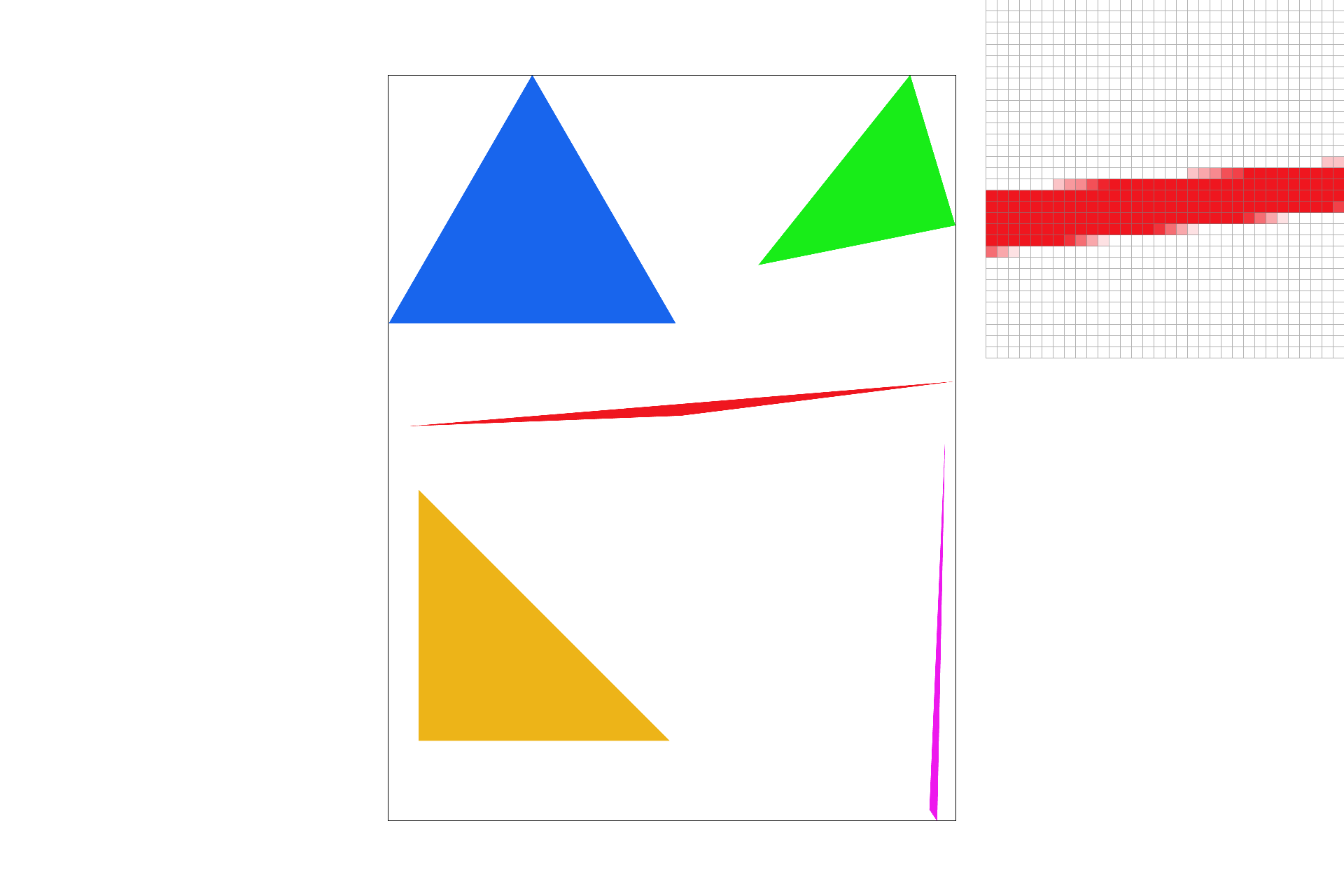 basic/test4.svg with sample rate of 16
basic/test4.svg with sample rate of 16
|
Part 3: Transforms
I implemented image transforms in part 3. By thinking of each transform as a 3x3 matrix, we can perform matrix-vector multiplication even though we are dealing with values that could be placed in a 2x2 matrix. Thus, we have an extra dummy node to help complete the matrix multiplication. This is known as homogenous coordinate transformations. After completing scale, rotate, and translate transforms, I was able to manipulate the robot image into a waving robot. I added multiple rotations, transformations, and changed the color of each cube to achieve this.
 transforms/robot.svg
transforms/robot.svg
|
 my waving robot!
my waving robot!
|
Section II: Sampling
Part 4: Barycentric coordinates
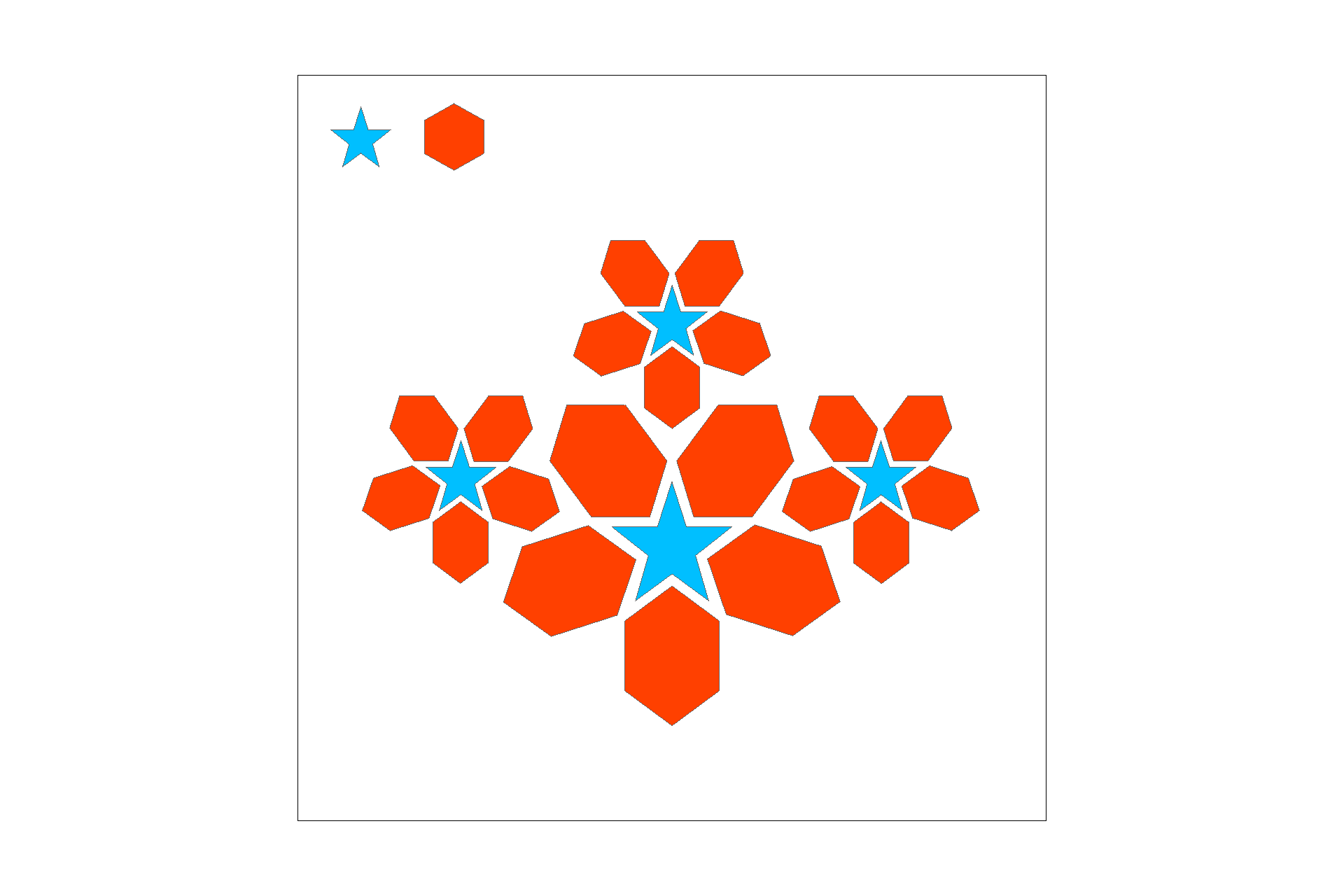
In part four, I used barycentric coordinates to determine where a point P lies relative to a set of triangle veritcies. The goal of using barycentric coordinates is to get a weighted sum for our pixel color. In order to average the color in part of an image(for a smooth gradient), we can take 3 values: alpha, beta, and gamma (alpha + beta + gamma = 1). Interpolating between these values and triangle verticies gives the color at position P. This gradient between colors at verticies can be seen in the trangle below.
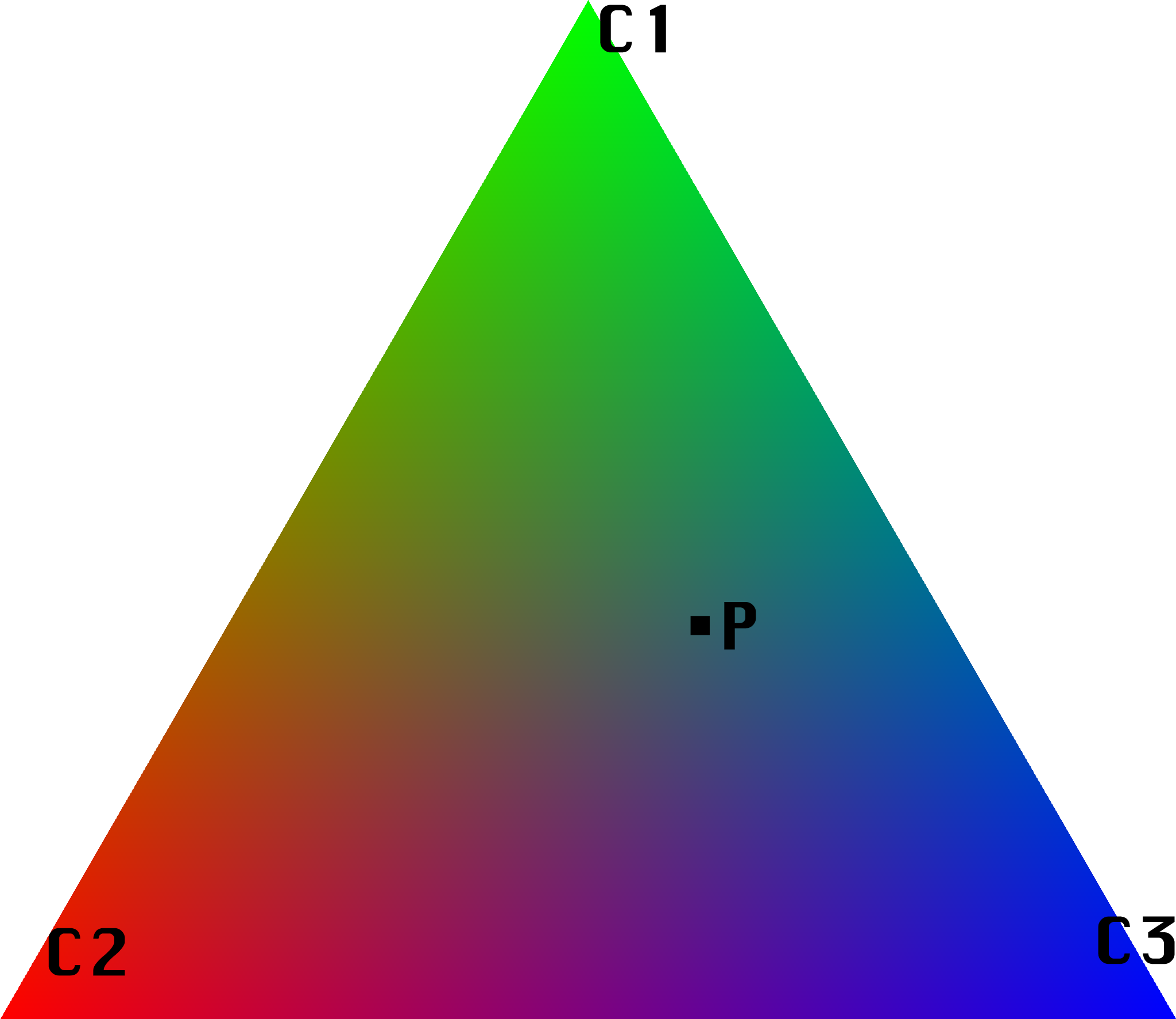 Triangle with R, G, & B weighted verticies
Triangle with R, G, & B weighted verticies
|
 basic/test7.svg
basic/test7.svg
|
Part 5: "Pixel sampling" for texture mapping
Part five included the implementation of nearest-neighbor sampling and bilinear sampling for texture mapping. Nearest-pixel sampling uses the closest texel value for a given pixel's color value, whereas bilinear sampling uses the weighted average of the nearest four texels. With nearest-neighbor sampling, I sampled at the closest texel to each (u, v) point. I found the minimum distance from (u, v) to the 4 nearest texel center points and I selected the color at that minimum distance texel. For bilinear sampling, I interpolated between the nearest vertical and horizontal texel centers to my (u, v) point. By calculating the Barycentric coordinates in both x & y directions, as described in part 5, I got the R, G, & B values at the (u, v) coordinate. Below is a good example of where bilinear defeats nearest neighbor sampling: the lines are more fluid and continuous. If the source image is lower resolution, nearest-neighbor will select values less accurately, but in a high-resolution image, bilinear and nearest-neigbor are very similar.
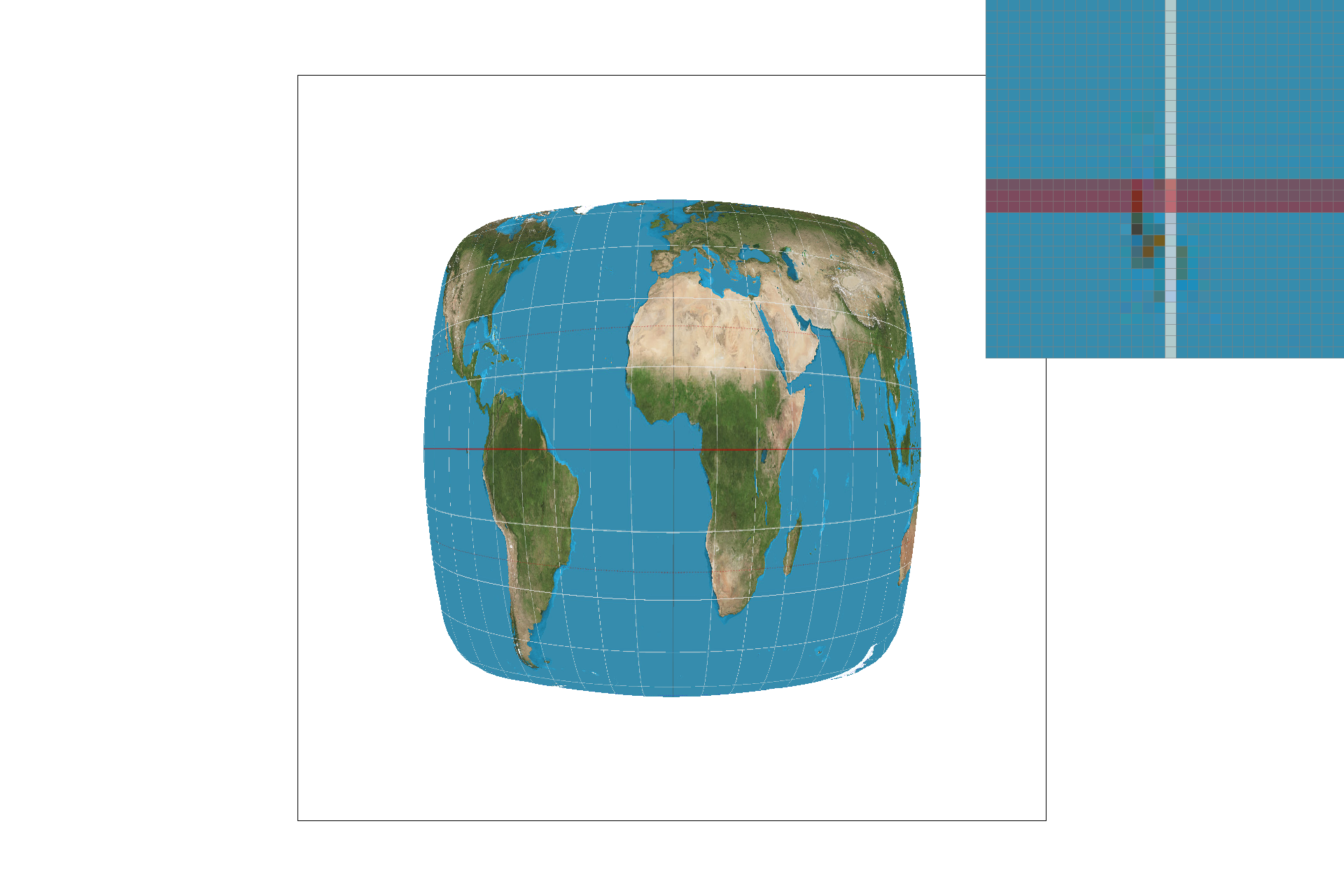 bilinear
bilinear
|
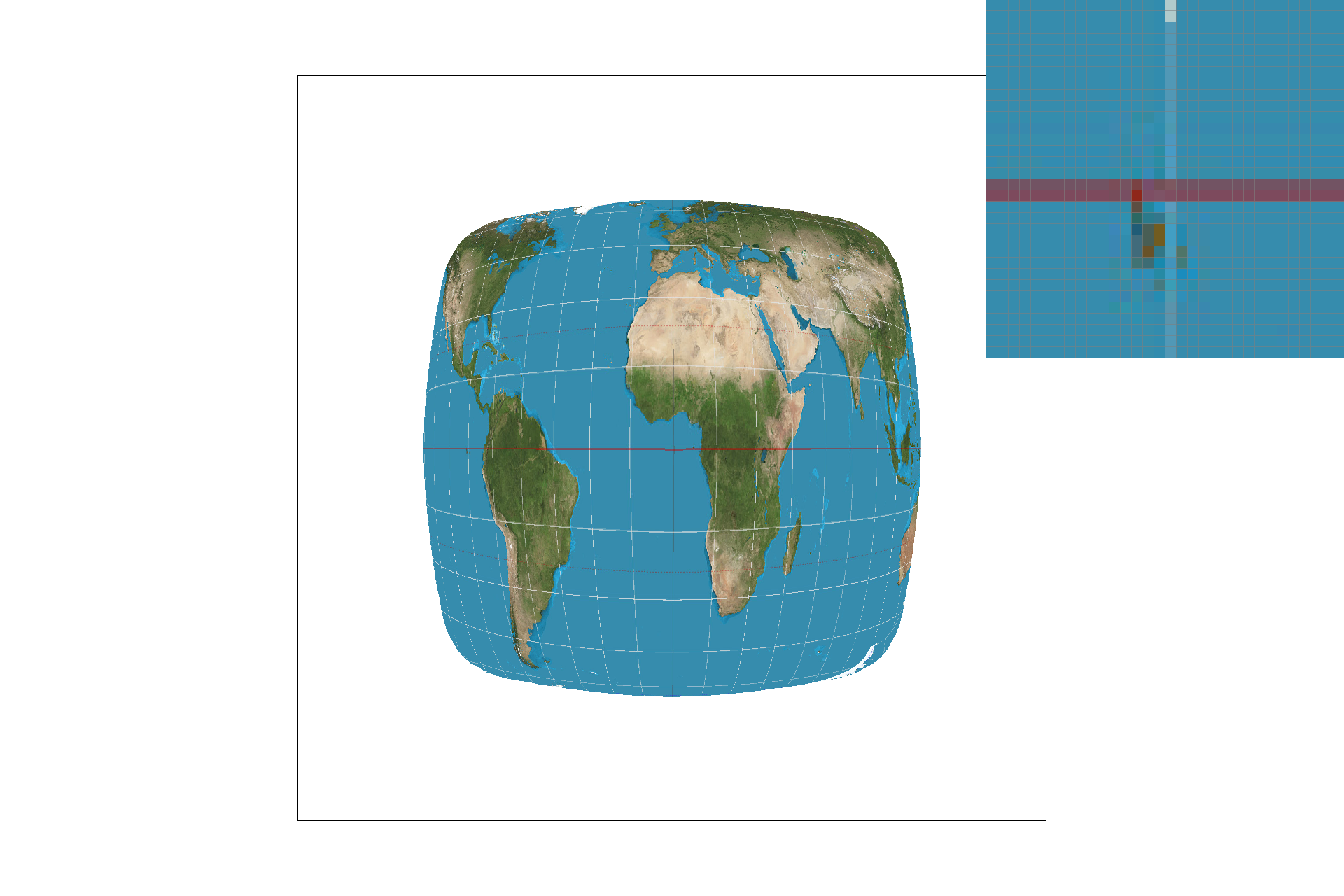 nearest-pixel
nearest-pixel
|
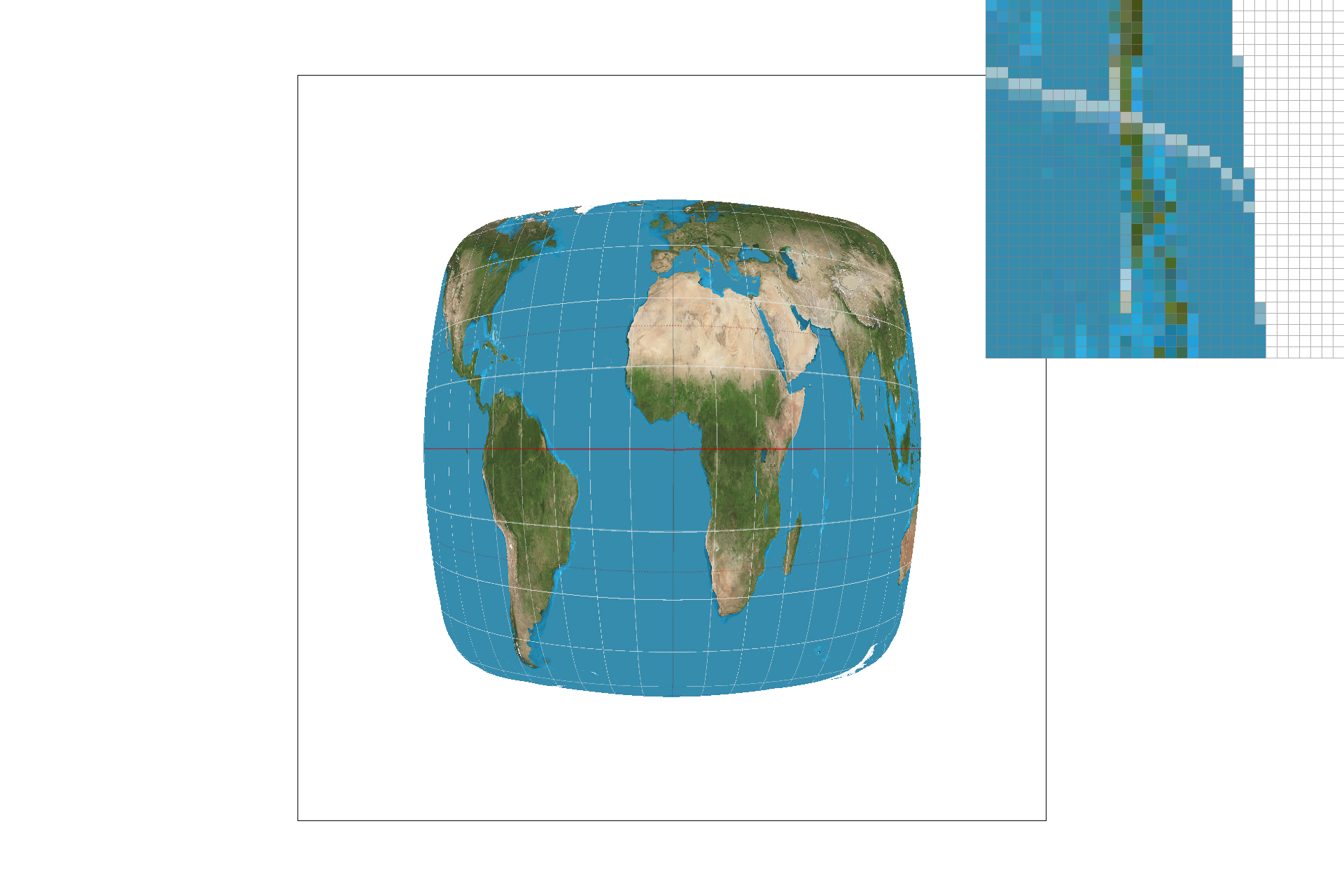 texmap/test1.svg nearest-pixel sampling, sample rate 1
texmap/test1.svg nearest-pixel sampling, sample rate 1
|
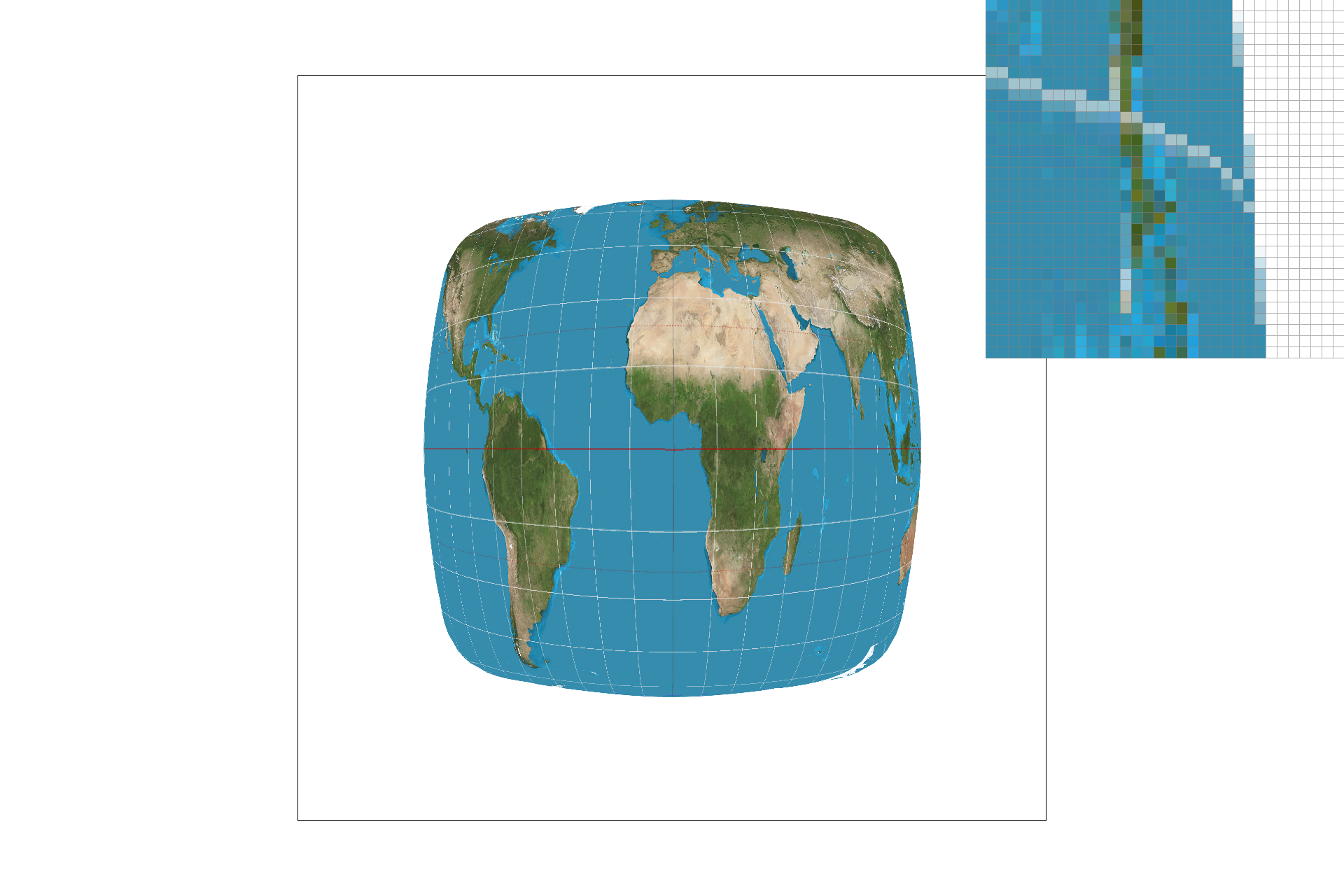 texmap/test1.svg nearest-pixel sampling, sample rate 16
texmap/test1.svg nearest-pixel sampling, sample rate 16
|
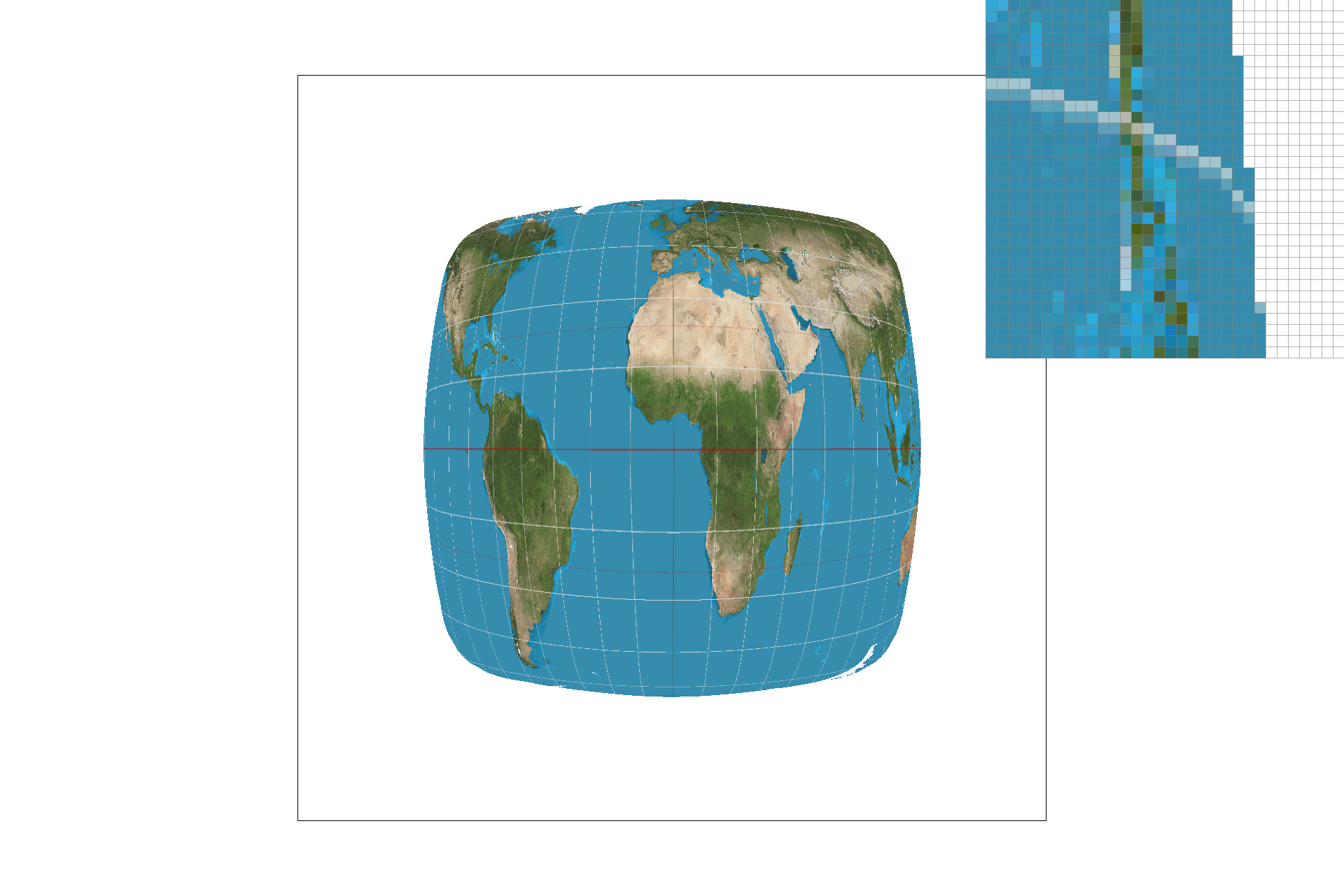 texmap/test1.svg bilinear sampling, sample rate 1
texmap/test1.svg bilinear sampling, sample rate 1
|
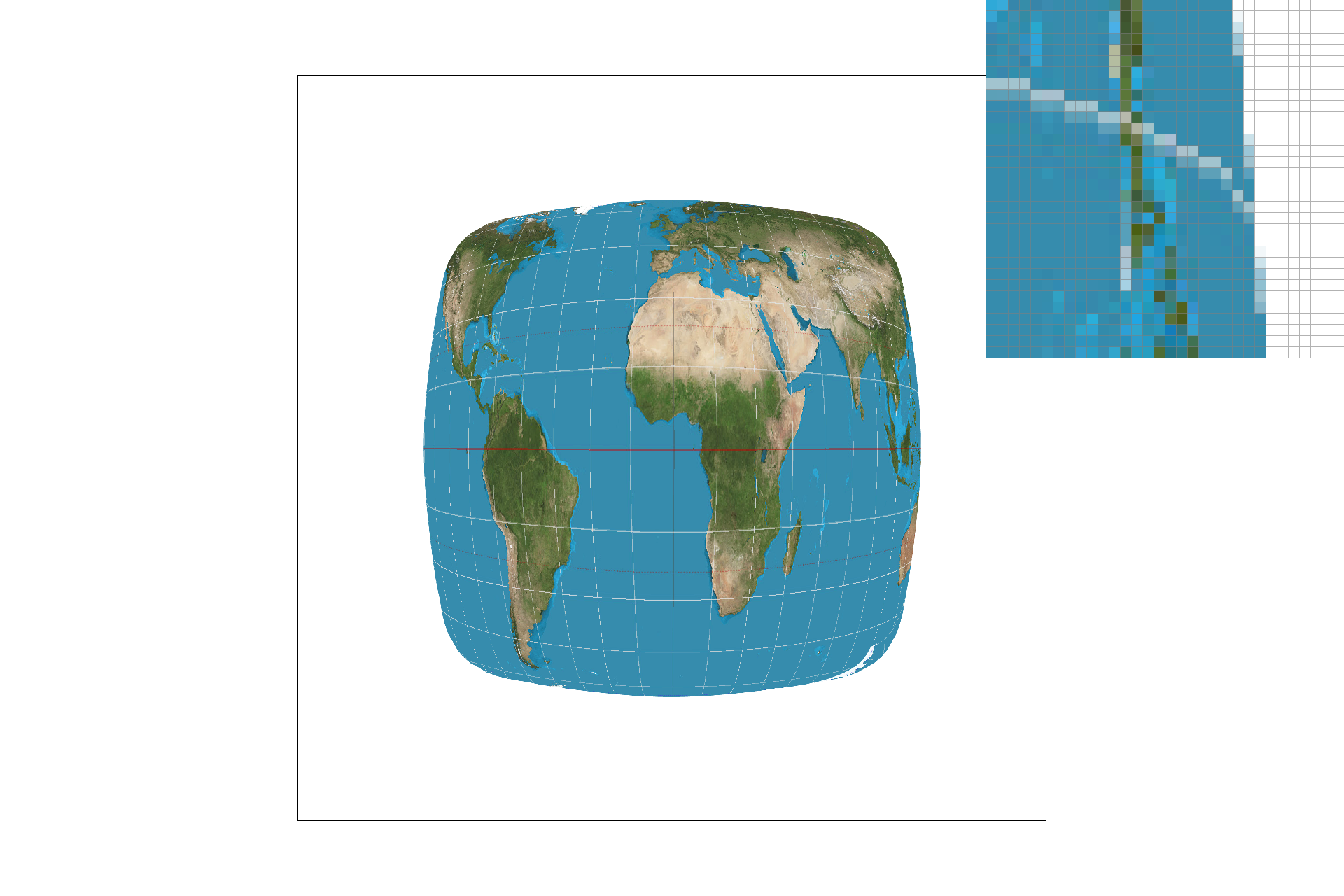 texmap/test1.svg bilinear sampling, sample rate 16
texmap/test1.svg bilinear sampling, sample rate 16
|
Part 6: "Level sampling" with mipmaps for texture mapping
In part 6, I added the functionalies of level sampling with mipmaps. Mipmapping essentially prefilters the texture and stores it in smaller pixel sizes. Calculating barycentric coordinates of (x+1,y)(x+1,y) & (x,y+1)(x,y+1) are necessary for finding the (du/dx, dv/dx) & (du/dy, dv/dy) to calculate the correct mipmap level. Once the barycentric coordinates are calculated in the rasterize function, the (u, v) coordinates are calculated for these p_dx & p_dy coords in a similar way as calculated in pixel sampling above. Finally, I calculated difference vectors with these (u, v) coordinate sets and scaled them by the with and height of the texture image. The level is calculated by taking log2(max(difference vectors)). While using mipmap requires less memory as the level increases, the resolution and clarity of the mapped texture decreases. It does, however, increase rendering speed and decrease aliasing. Overall, bilinear sampling has the most antialiasing capability, but is the least efficient. Below, I used my own texture to show how each of the texture mapping combinations differ.
 Original Image
Original Image
|
 level zero, nearest pixel sampling
level zero, nearest pixel sampling
|
 level zero, bilinear sampling
level zero, bilinear sampling
|
 nearest level, nearest pixel sampling
nearest level, nearest pixel sampling
|
 nearest level, bilinear sampling
nearest level, bilinear sampling
|